EXPERIMENTAL PROTOCOL
Ground Truth
Reference measurements have been made by a Qualisys system. This technology provides quaternions with a precision of 0.5° of rotation. Our room is equipped with 20 Oqus cameras connected to a server and a Qualisys Tracker software
with a sampling rate at 150Hz. For the purpose of aligning timestamps of our ground truth data with the one of smartphone’s sensors, we used a slerp interpolation [1]. The motion tracker reference frame has been aligned with EF using room orientation provided by architects. The room is a 10m×10m square motion lab.

Figure 1. Kinovis room at Inria, Grenoble, France
A smartphone handler with infrared markers has been created with a 3D printer for this study and its markers have
been aligned with sensor frame.
Typical Smartphone Motions
We identify 8 typical motions for a smartphone, inspired from [2].

Querying the context in augmented reality

Walking while user is texting a message

Walking while the user is phoning

Walking with a swinging hand

Walking with the device in the front pocket

Walking with the device in the back pocket

Running with the device in the hand

Running with the device in the pocket
Figure 2. The eight typical motions for a smartphone.
Each motion comes with particular external accelerations. The Table 1 shows some statistics on external acceleration magnitude grouped by motion, for the 126 tests. For the last 3 columns, No det. means our reference system detected an high external acceleration but the detector of Eq.(15) not. The inverse is not possible.
| Motions |
MAE
(m.s-2) |
MAE Estimated
(m.s-2) |
Ratio |
STD
(m.s-2) |
> 0.5 m.s-2 |
> 1.5 m.s-2 |
> 5 m.s-2 |
No det. > 0.5 m.s-2 |
No det. > 1.5 m.s-2 |
No det. > 5 m.s-2 |
| AR | 0.56 | 0.24 | 2.39 | 0.34 | 46.4% | 2.4% | 0.0% | 35.2% | 1.9% | 0.0% |
| Texting | 1.08 | 0.61 | 1.81 | 0.59 | 83.5% | 20.7% | 0.1% | 39.0% | 12.7% | 0.1% |
| Phoning | 1.08 | 0.57 | 1.96 | 0.60 | 83.1% | 21.0% | 0.1% | 43.2% | 13.5% | 0.1% |
| Front Pocket | 2.48 | 1.40 | 1.81 | 1.58 | 97.1% | 68.2% | 7.5% | 30.6% | 35.8% | 4.0% |
| Back Pocket | 2.53 | 1.23 | 2.10 | 1.56 | 97.5% | 72.0% | 7.7% | 33.3% | 46.4% | 4.3% |
| Swinging | 5.28 | 2.30 | 2.42 | 1.82 | 99.7% | 96.8% | 52.5% | 15.3% | 39.1% | 43.2% |
| Running Pocket | 9.56 | 5.93 | 1.61 | 4.53 | 99.6% | 98.2% | 84.4% | 4.7% | 12.4% | 31.5% |
| Running Hand | 16.34 | 8.44 | 2.02 | 5.25 | 99.9% | 99.7% | 98.6% | 5.7% | 16.4% | 42.9% |
Table 1. Statistics on Magnitude of External Accelerations.
During our tests, we observed that external accelerations are almost never zeros because the device is always moving and it is almost impossible to produce a constant speed for the device when it is held or carried in a pocket. However, we noticed a high variety of external accelerations: some motions involve external accelerations that are 20 times lower than gravity while others (like running hand) are closer to twice the value of gravity. We also noticed that the maximum swing of accelerometer (±2g) is often reached during our running experiments.
Introducing Magnetic Perturbations
During tests in several buildings, we noticed that indoorenvironments are always more or less disturbed. This is mainly due to building structure. We also observed in some cases, if user is close to heaters, electrical cabinets or simply close to a wall, magnitude of magnetic field can grow up to 150 µT during few seconds, that is 3 times more than Earth’s magnetic field (see e.g. Figure 3).
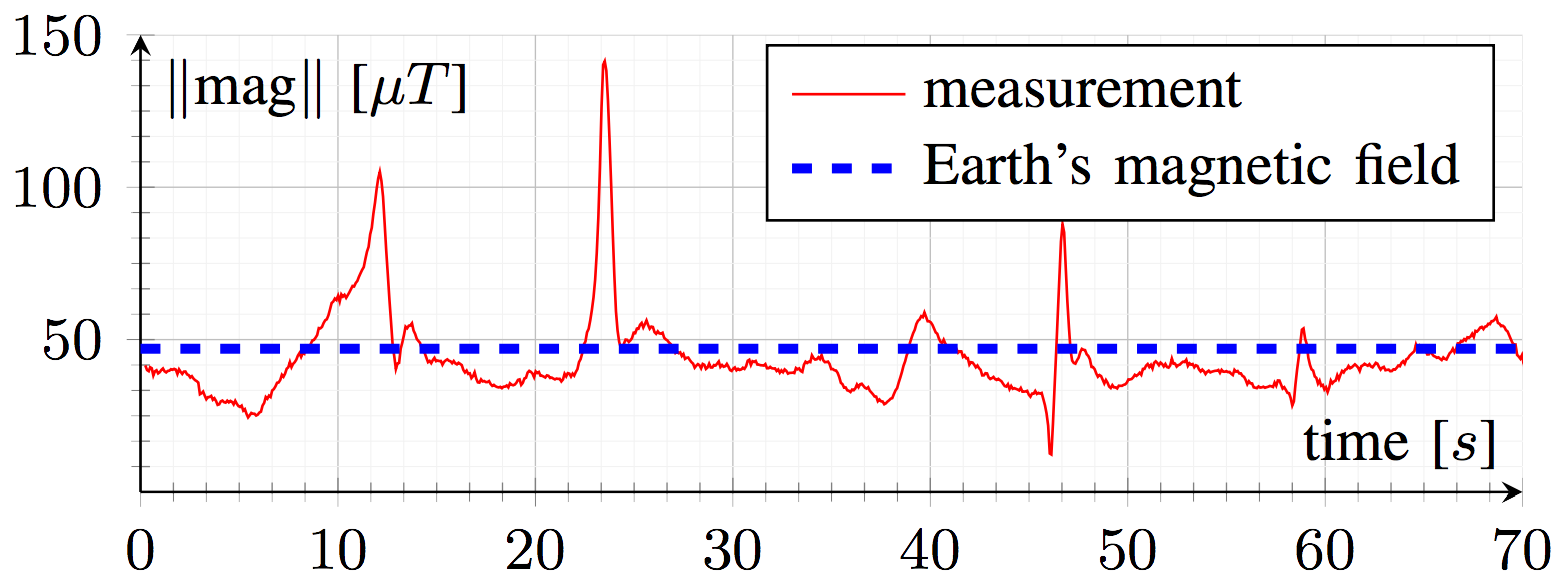
Figure 3. Magnitude of magnetic field measurements and Earth’s magnetic field in the indoor environment of Inria building in Grenoble.
The motion capture system that we use is located in a room with low and constant magnetic perturbations. In order to reproduce typical magnetic perturbations of indoor environments inside the motion lab, we used several magnetic boards. This allowed us to introduce magnetic perturbations similar to the ones described above. Specifically, during the 2 minutes tests, we brought the device to a few centimeters away from magnetic boards; and we repeated this action 3 or 4 times.

Figure 4. Magnetic boards for building structure and heaters simulation
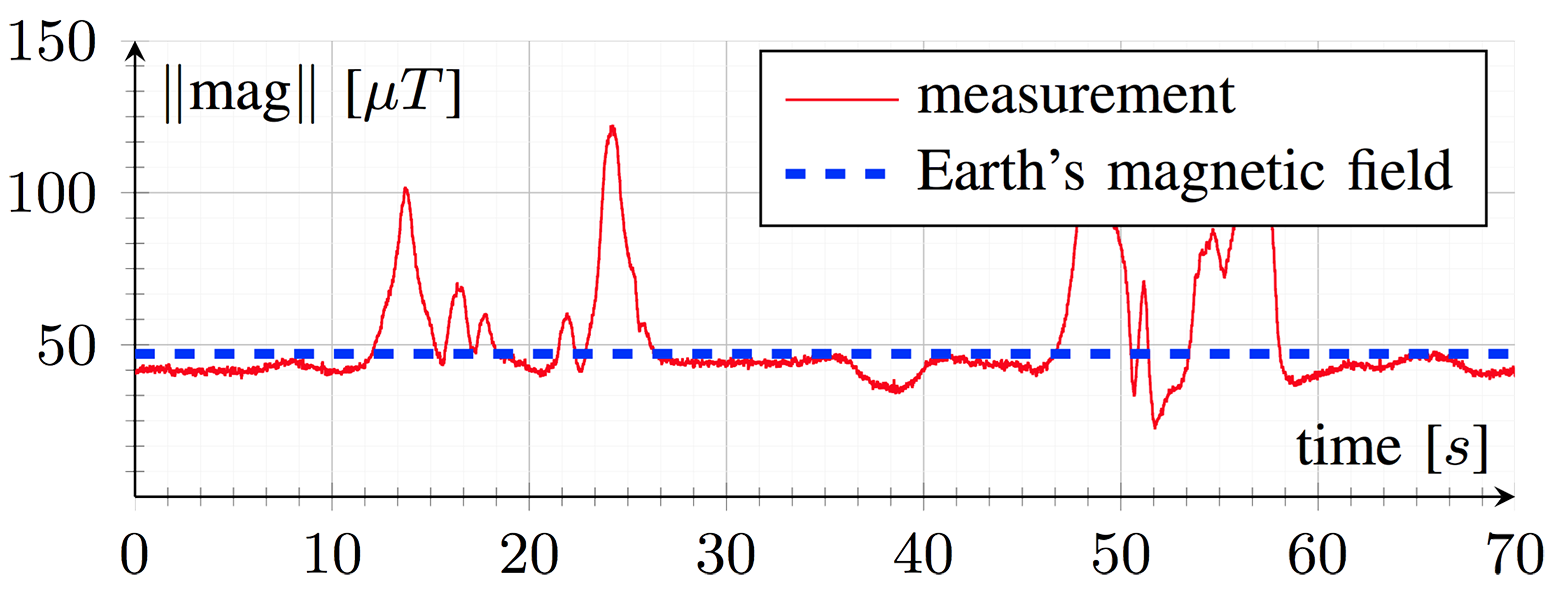
Figure 5. Magnitude of magnetic field measurements and Earth’s magnetic field during our simulation with magnetic boards.
The Table 2 shows some statistics on external magnetic field magnitude. For the last 3 columns,
No det. means our reference system detected an high external acceleration but the detector of Eq.(16) not. The inverse is not possible.
| Perturbations |
MAE
(μT) |
MAE Estimated
(μT) |
Ratio |
STD
(μT) |
> 10 μT |
> 15 μT |
> 20 μT |
No det. > 10 μT |
No det. > 15 μT |
No det. > 20 μT |
| With | 29.57 | 18.61 | 1.65 | 43.09 | 46.7% | 31.2% | 26.5% | 20.4% | 12.5% | 9.9% |
| Without | 7.12 | 5.18 | 1.40 | 1.99 | 13.0% | 0.2% | 0.0% | 9.0% | 0.1% | 0.0% |
Table 2. Statistics on Magnitude of External Magnetic Fields.
Different Devices
Measurements have been recorded with 3 different smartphones from 2 manufacturers. The 3 smartphones used are a LG Nexus 5, an iPhone 5 and an iPhone 4S. We implemented a log application for Android and iOS. Table 3 summarizes sensors specifications for the 3 devices.
|
Accelerometer |
Gyroscope |
Magnetometer |
| iPhone 4S |
ST Micro STM33DH
100Hz |
ST Micro AGDI
100Hz |
AKM 8975
40Hz |
| iPhone 5 |
ST Micro LIS331DLH
100Hz |
ST Micro L3G4200D
100Hz |
AKM 8963
25Hz |
| Nexus 5 |
InvenSense MPU6515
200Hz |
InvenSense MPU6515
200Hz |
AKM 8963
60Hz |
Table 3. Sensors specifications with the maximum sampling rate.
For the purpose of aligning timestamps of magnetic field and gyroscope data with data obtained from accelerometer, we used a linear extrapolation. In order to keep the focus on a realtime process, interpolation is not allowable here. We choose to align data at 100Hz. Moreover, for each experience, we chose to process 31 algorithms at 4 sampling rates and with 7 different calibrations, that is a total of more than 110 000 tests and 804 millions quaternions compared.
Common Basis of Comparison and Reproduction
To ensure a reasonably fast convergence of algorithms, we initialize the first quaternion using the first measurement of accelerometer and the first measurement of magnetometer (see Algorithm 1). In addition, we discard the first five seconds from our results.
H = cross(mag, acc);
H = H/norm(H);
acc = acc/norm(acc);
M = cross(acc, H);
% ENU
R = [ H(1) M(1) acc(1)
H(2) M(2) acc(2)
H(3) M(3) acc(3)];
% NED
% R = [ M(1) H(1) -acc(1)
% M(2) H(2) -acc(2)
% M(3) H(3) -acc(3)];
q = dcm2quat(R);
Algorithm 1. Initialization using first measurement of magnetometer and accelerometer.
Most smartphone APIs (including Nexus 5 and iPhones) provide both calibrated and uncalibrated data from magnetometer and gyroscope (not from iOS API), and only uncalibrated data from accelerometer. Calibration phases can be triggered by the Android operating system at anytime. However, we notice that the gyroscope bias is removed during static phases and the magnetometer is calibrated during the drawing of an infinity symbol. For iOS devices, magnetometer calibration must be explicitly triggered by the user. The exact calibration algorithms embedded in both iOS and Android are not disclosed so we consider them as "black-boxes".
To investigate the impact of calibration, we also developed a custom calibration procedure: every morning, we applied our own implementation of the calibration based on Bartz et al. [3] to remove soft and hard iron distortions from magnetometer and based on Frosio et al. [4] for the accelerometer. In addition, for all calibrations we applied a scale to adjust magnitude to 9.8 m.s-2 for accelerometer and Earth's magnetic field magnitude for magnetometer. For the gyroscope, we simply remove the bias by subtracting measured values in each axis during static phases.
The precision error is reported using the Mean Absolute Error (MAE) on the Quaternion Angle Difference (QAD) [5]. It allows to avoid the use of Euler angles with the gimbal-lock problem. The formula of QAD is defined by:
θ = cos-1 ( 2 ⟨ q1, q2 ⟩2 - 1).
Since the accuracy of the system that provides the ground truth is ± 0.5°, we consider that two algorithms exhibiting differences in precision lower than 0.5° rank similarly.
RESULTS
Importance of Calibration
|
Mag: No
Gyr: No
Acc: No |
Mag: Yes
Gyr: No
Acc: No |
Mag: Yes
Gyr: No
Acc: Yes |
Mag: Yes
Gyr: Yes
Acc: No |
Mag: Yes
Gyr: Yes
Acc: Yes |
Mag: Yes
Gyr: OS*
Acc: Yes |
Mag: OS
Gyr: OS*
Acc: No |
| Choukroun |
95.1° |
16.5° |
16.5° |
9.9° |
10.0° |
9.9° |
17.3° |
| ChoukrounSn |
82.5° |
52.6° |
52.5° |
19.3° |
19.0° |
17.9° |
41.2° |
| Ekf |
79.8° |
19.4° |
19.4° |
7.9° |
8.0° |
7.9° |
18.2° |
| EkfExp |
79.5° |
19.5° |
19.5° |
8.0° |
8.0° |
7.9° |
18.2° |
| EkfLJ |
82.3° |
19.4° |
19.4° |
8.0° |
8.0° |
8.0° |
18.0° |
| EkfRev |
81.5° |
17.2° |
17.3° |
8.3° |
8.4° |
8.4° |
17.7° |
| EkfRevSn |
91.2° |
74.9° |
74.6° |
57.8° |
57.8° |
56.3° |
67.0° |
| EkfSn |
88.5° |
70.0° |
70.9° |
36.4° |
35.8° |
36.0° |
58.3° |
| Fourati |
83.7° |
15.6° |
15.5° |
10.3° |
10.4° |
10.4° |
16.3° |
| FouratiExtacc |
108.9° |
27.1° |
27.2° |
13.5° |
13.5° |
13.4° |
24.5° |
| FouratiMartin |
83.8° |
14.9° |
14.9° |
8.3° |
8.3° |
8.3° |
16.1° |
| FouratiMartinExtmagWtRep |
82.1° |
15.4° |
15.4° |
6.1° |
6.2° |
6.1° |
15.5° |
| Madgwick |
77.5° |
18.2° |
18.2° |
8.1° |
8.1° |
8.1° |
17.7° |
| MadgwickB |
91.6° |
13.4° |
13.3° |
13.1° |
13.1° |
13.1° |
18.7° |
| Mahony |
99.6° |
20.2° |
20.2° |
14.2° |
14.2° |
14.2° |
19.1° |
| MahonyB |
100.1° |
24.1° |
24.1° |
24.0° |
24.1° |
24.0° |
23.4° |
| MahonyMartin |
77.3° |
22.0° |
22.0° |
7.3° |
7.3° |
7.2° |
18.5° |
| MahonyMartinExtmagWtRep |
82.0° |
24.1° |
24.1° |
7.1° |
7.1° |
6.9° |
19.4° |
| Martin |
79.2° |
19.7° |
19.7° |
17.9° |
18.1° |
18.1° |
18.6° |
| MichelEkf |
79.8° |
19.4° |
19.4° |
7.9° |
8.0° |
7.9° |
18.2° |
| MichelEkfExtmag |
82.0° |
19.3° |
19.3° |
7.6° |
7.7° |
7.6° |
18.0° |
| MichelEkfExtmagWt |
82.0° |
19.4° |
19.4° |
7.1° |
7.2° |
7.1° |
18.0° |
| MichelEkfExtmagWtRep |
82.0° |
20.1° |
20.1° |
6.9° |
7.0° |
6.9° |
18.2° |
| MichelEkfSn |
88.5° |
70.0° |
70.9° |
36.4° |
35.8° |
36.0° |
58.3° |
| MichelObs |
83.7° |
15.6° |
15.5° |
10.3° |
10.4° |
10.4° |
16.3° |
| MichelObsExtmag |
82.1° |
13.4° |
13.3° |
7.7° |
7.7° |
7.7° |
15.5° |
| MichelObsExtmagWt |
82.1° |
13.6° |
13.6° |
7.1° |
7.1° |
7.1° |
15.2° |
| MichelObsExtmagWtRep |
82.1° |
13.6° |
13.5° |
5.9° |
5.9° |
5.9° |
15.1° |
| Renaudin |
82.2° |
19.5° |
19.5° |
8.0° |
8.1° |
8.0° |
18.1° |
| RenaudinB |
95.0° |
9.5° |
9.5° |
9.6° |
9.6° |
9.5° |
17.7° |
| RenaudinBG |
94.3° |
9.6° |
9.6° |
9.8° |
9.7° |
9.7° |
17.6° |
| RenaudinBGExtaccExtmag |
96.5° |
10.3° |
10.3° |
10.5° |
10.4° |
10.3° |
18.5° |
| RenaudinExtacc |
86.2° |
20.2° |
20.2° |
8.9° |
8.9° |
8.9° |
19.5° |
| RenaudinExtaccExtmag |
84.6° |
20.2° |
20.2° |
8.7° |
8.8° |
8.7° |
19.4° |
| RenaudinExtmag |
81.3° |
19.5° |
19.5° |
7.8° |
7.9° |
7.8° |
18.0° |
| RenaudinSn |
81.7° |
53.1° |
52.9° |
20.3° |
20.1° |
19.1° |
42.4° |
| Sabatini |
79.8° |
19.4° |
19.4° |
7.9° |
8.0° |
7.9° |
18.2° |
| SabatiniExtacc |
100.6° |
25.2° |
25.3° |
10.8° |
10.8° |
10.7° |
22.8° |
| SabatiniExtaccExtmag |
100.6° |
25.2° |
25.3° |
10.8° |
10.8° |
10.7° |
22.8° |
| SabatiniExtmag |
81.0° |
19.3° |
19.3° |
7.7° |
7.7° |
7.7° |
17.8° |
Table 4. Precision of attitude estimation according to calibration with all motions.
The Difficulty with Noise for Kalman Filters
|
AR |
Texting |
Phoning |
Front
Pocket |
Back
Pocket |
Swinging |
Running
Pocket |
Running
Hand |
| Choukroun |
5.1° |
4.3° |
4.4° |
4.8° |
4.6° |
6.3° |
7.9° |
21.1° |
| ChoukrounSn |
15.6° |
20.6° |
15.9° |
17.8° |
16.9° |
11.5° |
17.6° |
35.2° |
| Ekf |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| EkfRev |
4.5° |
3.8° |
3.8° |
4.7° |
4.6° |
6.3° |
8.5° |
14.1° |
| EkfRevSn |
73.3° |
95.8° |
55.2° |
32.9° |
36.0° |
75.7° |
24.8° |
69.1° |
| EkfSn |
44.0° |
57.8° |
36.1° |
20.6° |
30.8° |
29.1° |
23.3° |
54.1° |
| MichelEkf |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| MichelEkfSn |
44.0° |
57.8° |
36.1° |
20.6° |
30.8° |
29.1° |
23.3° |
54.1° |
| Renaudin |
4.5° |
3.8° |
3.7° |
4.7° |
4.6° |
6.1° |
8.5° |
17.9° |
| RenaudinSn |
20.8° |
18.5° |
17.8° |
17.3° |
18.4° |
11.4° |
17.4° |
36.5° |
Table 5. Precision of attitude estimation according to sensor noises without magnetic perturbations.
Bias Consideration
|
AR |
Texting |
Phoning |
Front
Pocket |
Back
Pocket |
Swinging |
Running
Pocket |
Running
Hand |
| Madgwick |
4.8° |
4.1° |
4.6° |
4.9° |
5.0° |
5.8° |
7.1° |
16.5° |
| MadgwickB |
5.2° |
4.8° |
5.4° |
5.8° |
6.2° |
11.5° |
10.5° |
19.8° |
| Mahony |
5.0° |
4.6° |
4.2° |
5.1° |
5.2° |
7.5° |
7.9° |
11.2° |
| MahonyB |
5.6° |
4.9° |
4.7° |
6.1° |
5.7° |
9.9° |
13.1° |
26.4° |
| Renaudin |
4.5° |
3.8° |
3.7° |
4.7° |
4.6° |
6.1° |
8.5° |
17.9° |
| RenaudinB |
4.5° |
3.6° |
3.7° |
4.5° |
4.6° |
7.0° |
12.7° |
19.3° |
| RenaudinBG |
4.5° |
3.7° |
3.8° |
4.5° |
4.6° |
6.9° |
12.8° |
19.3° |
Table 6. Precision of attitude according to bias estimation without magnetic perturbations.
Behaviors during Typical Smartphone Motions
|
AR |
Texting |
Phoning |
Front
Pocket |
Back
Pocket |
Swinging |
Running
Pocket |
Running
Hand |
| Choukroun |
5.1° |
4.3° |
4.4° |
4.8° |
4.6° |
6.3° |
7.9° |
21.1° |
| ChoukrounSn |
15.6° |
20.6° |
15.9° |
17.8° |
16.9° |
11.5° |
17.6° |
35.2° |
| Ekf |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| EkfExp |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
6.0° |
8.3° |
17.0° |
| EkfLJ |
4.5° |
3.8° |
3.7° |
4.7° |
4.6° |
6.1° |
8.5° |
17.6° |
| EkfRev |
4.5° |
3.8° |
3.8° |
4.7° |
4.6° |
6.3° |
8.5° |
14.1° |
| EkfRevSn |
73.3° |
95.8° |
55.2° |
32.9° |
36.0° |
75.7° |
24.8° |
69.1° |
| EkfSn |
44.0° |
57.8° |
36.1° |
20.6° |
30.8° |
29.1° |
23.3° |
54.1° |
| Fourati |
4.8° |
4.0° |
4.4° |
4.6° |
4.8° |
5.3° |
6.3° |
6.6° |
| FouratiExtacc |
4.9° |
5.4° |
4.7° |
6.0° |
5.7° |
8.4° |
12.2° |
29.1° |
| FouratiMartin |
4.6° |
3.4° |
4.3° |
4.5° |
4.6° |
5.5° |
6.4° |
11.2° |
| FouratiMartinExtmagWtRep |
4.6° |
3.4° |
4.3° |
4.5° |
4.6° |
5.5° |
6.4° |
11.2° |
| Madgwick |
4.8° |
4.1° |
4.6° |
4.9° |
5.0° |
5.8° |
7.1° |
16.5° |
| MadgwickB |
5.2° |
4.8° |
5.4° |
5.8° |
6.2° |
11.5° |
10.5° |
19.8° |
| Mahony |
5.0° |
4.6° |
4.2° |
5.1° |
5.2° |
7.5° |
7.9° |
11.2° |
| MahonyB |
5.6° |
4.9° |
4.7° |
6.1° |
5.7° |
9.9° |
13.1° |
26.4° |
| MahonyMartin |
4.7° |
3.9° |
4.0° |
4.7° |
4.5° |
5.1° |
7.4° |
18.5° |
| MahonyMartinExtmagWtRep |
4.7° |
4.0° |
4.0° |
4.7° |
4.5° |
5.1° |
7.4° |
18.5° |
| Martin |
4.7° |
4.5° |
5.3° |
6.4° |
6.8° |
12.6° |
12.0° |
19.3° |
| MichelEkf |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| MichelEkfExtmag |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| MichelEkfExtmagWt |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| MichelEkfExtmagWtRep |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
6.0° |
8.2° |
16.8° |
| MichelEkfSn |
44.0° |
57.8° |
36.1° |
20.6° |
30.8° |
29.1° |
23.3° |
54.1° |
| MichelObs |
4.8° |
4.0° |
4.4° |
4.6° |
4.8° |
5.3° |
6.3° |
6.6° |
| MichelObsExtmag |
4.8° |
4.0° |
4.4° |
4.6° |
4.8° |
5.3° |
6.3° |
6.6° |
| MichelObsExtmagWt |
4.8° |
4.0° |
4.4° |
4.6° |
4.8° |
5.3° |
6.3° |
6.6° |
| MichelObsExtmagWtRep |
4.8° |
3.9° |
4.4° |
4.6° |
4.8° |
5.3° |
6.3° |
6.6° |
| OS |
7.1° |
5.9° |
5.8° |
12.7° |
13.2° |
20.3° |
24.4° |
62.0° |
| Renaudin |
4.5° |
3.8° |
3.7° |
4.7° |
4.6° |
6.1° |
8.5° |
17.9° |
| RenaudinB |
4.5° |
3.6° |
3.7° |
4.5° |
4.6° |
7.0° |
12.7° |
19.3° |
| RenaudinBG |
4.5° |
3.7° |
3.8° |
4.5° |
4.6° |
6.9° |
12.8° |
19.3° |
| RenaudinBGExtaccExtmag |
4.5° |
3.7° |
3.8° |
4.3° |
4.7° |
6.9° |
12.3° |
31.8° |
| RenaudinExtacc |
4.5° |
3.8° |
3.7° |
4.8° |
4.8° |
6.0° |
8.0° |
30.3° |
| RenaudinExtaccExtmag |
4.5° |
3.8° |
3.7° |
4.8° |
4.8° |
6.0° |
8.0° |
30.3° |
| RenaudinExtmag |
4.5° |
3.8° |
3.7° |
4.7° |
4.6° |
6.1° |
8.5° |
17.9° |
| RenaudinSn |
20.8° |
18.5° |
17.8° |
17.3° |
18.4° |
11.4° |
17.4° |
36.5° |
| Sabatini |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
| SabatiniExtacc |
4.5° |
4.5° |
4.0° |
5.5° |
5.0° |
9.7° |
15.0° |
33.5° |
| SabatiniExtaccExtmag |
4.5° |
4.5° |
4.0° |
5.5° |
5.0° |
9.7° |
15.0° |
33.5° |
| SabatiniExtmag |
4.5° |
4.0° |
3.7° |
4.6° |
4.6° |
5.9° |
8.2° |
16.8° |
Table 7. Precision of Attitude estimation according to typical motions without magnetic perturbations.
Impact of Magnetic Perturbations
|
AR |
Texting |
Phoning |
Front
Pocket |
Back
Pocket |
Swinging |
| Choukroun |
24.8° |
13.3° |
12.4° |
11.0° |
9.6° |
10.1° |
| ChoukrounSn |
17.7° |
19.5° |
16.5° |
20.4° |
15.7° |
25.4° |
| Ekf |
16.6° |
10.1° |
8.9° |
8.0° |
7.0° |
8.6° |
| EkfExp |
16.6° |
10.1° |
9.0° |
7.9° |
7.0° |
8.7° |
| EkfLJ |
17.1° |
9.6° |
8.9° |
7.6° |
7.0° |
8.7° |
| EkfRev |
18.6° |
13.9° |
9.4° |
8.9° |
7.8° |
8.5° |
| EkfRevSn |
63.7° |
69.7° |
59.7° |
45.9° |
47.0° |
60.1° |
| EkfSn |
33.3° |
62.8° |
23.8° |
34.3° |
27.8° |
23.9° |
| Fourati |
32.1° |
19.1° |
14.6° |
16.4° |
14.0° |
8.8° |
| FouratiExtacc |
30.5° |
19.8° |
16.3° |
19.2° |
13.5° |
13.4° |
| FouratiMartin |
21.7° |
13.1° |
12.1° |
10.1° |
8.1° |
7.4° |
| FouratiMartinExtmagWtRep |
10.2° |
7.7° |
5.8° |
5.4° |
5.2° |
7.5° |
| Madgwick |
18.2° |
10.0° |
8.1° |
7.8° |
7.5° |
9.4° |
| MadgwickB |
39.3° |
20.7° |
15.0° |
15.7° |
10.6° |
13.2° |
| Mahony |
31.8° |
26.6° |
19.9° |
30.0° |
26.1° |
13.9° |
| MahonyB |
40.3° |
52.8° |
43.0° |
49.3° |
51.6° |
23.3° |
| MahonyMartin |
14.4° |
7.7° |
7.6° |
5.9° |
5.8° |
7.7° |
| MahonyMartinExtmagWtRep |
10.1° |
8.7° |
6.3° |
6.4° |
5.5° |
9.5° |
| Martin |
34.4° |
35.2° |
23.7° |
30.6° |
29.0° |
21.5° |
| MichelEkf |
16.6° |
10.1° |
8.9° |
8.0° |
7.0° |
8.6° |
| MichelEkfExtmag |
14.2° |
9.2° |
5.5° |
9.0° |
8.9° |
8.6° |
| MichelEkfExtmagWt |
12.3° |
8.7° |
5.3° |
7.2° |
6.3° |
8.5° |
| MichelEkfExtmagWtRep |
10.8° |
7.5° |
5.7° |
5.5° |
5.3° |
10.3° |
| MichelEkfSn |
33.3° |
62.8° |
23.8° |
34.3° |
27.8° |
23.9° |
| MichelObs |
32.1° |
19.1° |
14.6° |
16.4° |
14.0° |
8.8° |
| MichelObsExtmag |
18.0° |
10.3° |
7.4° |
11.4° |
11.9° |
8.8° |
| MichelObsExtmagWt |
15.5° |
10.2° |
7.1° |
9.7° |
9.3° |
7.4° |
| MichelObsExtmagWtRep |
10.7° |
7.7° |
5.8° |
6.0° |
5.4° |
7.1° |
| OS |
29.0° |
19.2° |
19.8° |
21.1° |
24.4° |
37.9° |
| Renaudin |
17.1° |
9.5° |
8.9° |
7.6° |
7.0° |
8.7° |
| RenaudinB |
20.7° |
17.5° |
9.3° |
11.3° |
7.4° |
8.3° |
| RenaudinBG |
20.8° |
17.7° |
10.3° |
11.4° |
7.5° |
8.2° |
| RenaudinBGExtaccExtmag |
20.4° |
17.3° |
8.5° |
10.5° |
7.4° |
9.5° |
| RenaudinExtacc |
17.1° |
9.6° |
8.9° |
7.8° |
7.3° |
8.8° |
| RenaudinExtaccExtmag |
16.8° |
8.9° |
8.4° |
7.4° |
6.6° |
8.4° |
| RenaudinExtmag |
16.8° |
8.9° |
8.4° |
7.3° |
6.4° |
8.4° |
| RenaudinSn |
18.4° |
19.0° |
19.0° |
23.4° |
16.5° |
27.5° |
| Sabatini |
16.6° |
10.1° |
8.9° |
8.0° |
7.0° |
8.6° |
| SabatiniExtacc |
16.7° |
10.9° |
9.3° |
9.9° |
9.2° |
12.9° |
| SabatiniExtaccExtmag |
16.7° |
10.9° |
9.3° |
9.9° |
9.2° |
12.9° |
| SabatiniExtmag |
14.6° |
9.0° |
6.4° |
8.9° |
8.7° |
8.4° |
Table 8. Precision of attitude estimation according to typical motions with magnetic perturbations.
Comparison with Device-Embedded Algorithms
|
iPhone 4S |
iPhone 5 |
Nexus 5 |
| Choukroun |
8.6° |
10.4° |
10.9° |
| ChoukrounSn |
14.3° |
21.4° |
21.3° |
| Ekf |
6.7° |
8.7° |
8.5° |
| EkfExp |
6.7° |
8.8° |
8.5° |
| EkfLJ |
6.8° |
8.8° |
8.5° |
| EkfRev |
7.0° |
8.6° |
9.5° |
| EkfRevSn |
54.1° |
57.4° |
61.8° |
| EkfSn |
27.8° |
33.6° |
46.1° |
| Fourati |
8.8° |
10.3° |
12.1° |
| FouratiExtacc |
10.6° |
14.4° |
15.6° |
| FouratiMartin |
6.9° |
8.5° |
9.6° |
| FouratiMartinExtmagWtRep |
5.3° |
7.2° |
6.0° |
| Madgwick |
7.1° |
8.7° |
8.6° |
| MadgwickB |
11.1° |
13.3° |
14.9° |
| Mahony |
10.8° |
15.2° |
16.6° |
| MahonyB |
18.4° |
27.8° |
26.0° |
| MahonyMartin |
6.0° |
8.2° |
7.6° |
| MahonyMartinExtmagWtRep |
5.5° |
8.7° |
7.1° |
| Martin |
14.8° |
19.0° |
20.5° |
| MichelEkf |
6.7° |
8.7° |
8.5° |
| MichelEkfExtmag |
6.4° |
8.9° |
7.8° |
| MichelEkfExtmagWt |
6.0° |
8.5° |
7.1° |
| MichelEkfExtmagWtRep |
5.6° |
8.3° |
7.0° |
| MichelEkfSn |
27.8° |
33.6° |
46.1° |
| MichelObs |
8.8° |
10.3° |
12.1° |
| MichelObsExtmag |
6.9° |
8.3° |
8.1° |
| MichelObsExtmagWt |
6.3° |
7.6° |
7.4° |
| MichelObsExtmagWtRep |
5.4° |
6.5° |
5.9° |
| OS |
23.6° |
28.6° |
12.7° |
| Renaudin |
6.8° |
8.8° |
8.6° |
| RenaudinB |
9.1° |
8.7° |
10.9° |
| RenaudinBG |
9.2° |
8.7° |
11.2° |
| RenaudinBGExtaccExtmag |
8.7° |
10.5° |
12.0° |
| RenaudinExtacc |
6.9° |
10.7° |
9.2° |
| RenaudinExtaccExtmag |
6.8° |
10.5° |
9.0° |
| RenaudinExtmag |
6.6° |
8.6° |
8.4° |
| RenaudinSn |
16.1° |
23.2° |
21.1° |
| Sabatini |
6.7° |
8.7° |
8.5° |
| SabatiniExtacc |
8.7° |
12.4° |
11.2° |
| SabatiniExtaccExtmag |
8.7° |
12.4° |
11.2° |
| SabatiniExtmag |
6.4° |
8.9° |
7.9° |
Table 9. Precision according to device with all motions and with/without magnetic perturbations.
Empirical Computational Complexity
Figure 6. Relative performance in terms of CPU cost (lower is better).
Relevant Sampling Rates
|
100 Hz |
40 Hz |
10 Hz |
2 Hz |
| Choukroun |
10.0° |
10.1° |
15.6° |
34.7° |
| ChoukrounSn |
19.0° |
19.3° |
34.2° |
83.4° |
| Ekf |
8.0° |
8.1° |
15.3° |
49.5° |
| EkfExp |
8.0° |
8.1° |
15.6° |
51.7° |
| EkfLJ |
8.0° |
8.1° |
14.8° |
48.5° |
| EkfRev |
8.4° |
8.4° |
14.3° |
45.0° |
| EkfRevSn |
57.8° |
47.1° |
49.4° |
89.5° |
| EkfSn |
35.8° |
34.3° |
44.1° |
90.3° |
| Fourati |
10.4° |
10.4° |
18.9° |
52.5° |
| FouratiExtacc |
13.5° |
13.8° |
23.1° |
59.1° |
| FouratiMartin |
8.3° |
8.3° |
16.6° |
52.4° |
| FouratiMartinExtmagWtRep |
6.2° |
6.1° |
14.8° |
53.4° |
| Madgwick |
8.1° |
8.1° |
17.3° |
62.8° |
| MadgwickB |
13.1° |
13.6° |
21.9° |
63.0° |
| Mahony |
14.2° |
14.3° |
19.7° |
48.9° |
| MahonyB |
24.1° |
24.8° |
28.6° |
56.2° |
| MahonyMartin |
7.3° |
7.2° |
16.5° |
56.7° |
| MahonyMartinExtmagWtRep |
7.1° |
7.1° |
16.6° |
58.3° |
| Martin |
18.1° |
18.0° |
21.7° |
49.7° |
| MichelEkf |
8.0° |
8.1° |
15.3° |
49.5° |
| MichelEkfExtmag |
7.7° |
7.8° |
14.9° |
49.6° |
| MichelEkfExtmagWt |
7.2° |
7.3° |
14.6° |
49.8° |
| MichelEkfExtmagWtRep |
7.0° |
7.1° |
14.8° |
51.3° |
| MichelEkfSn |
35.8° |
34.3° |
44.1° |
90.3° |
| MichelObs |
10.4° |
10.4° |
18.9° |
52.5° |
| MichelObsExtmag |
7.7° |
7.7° |
16.1° |
50.7° |
| MichelObsExtmagWt |
7.1° |
7.1° |
15.7° |
51.0° |
| MichelObsExtmagWtRep |
5.9° |
6.0° |
14.8° |
52.5° |
| Renaudin |
8.1° |
8.2° |
15.5° |
51.2° |
| RenaudinB |
9.6° |
9.3° |
15.4° |
51.2° |
| RenaudinBG |
9.7° |
9.4° |
15.4° |
51.2° |
| RenaudinBGExtaccExtmag |
10.4° |
9.8° |
17.9° |
57.9° |
| RenaudinExtacc |
8.9° |
9.6° |
18.6° |
55.4° |
| RenaudinExtaccExtmag |
8.8° |
9.2° |
17.9° |
57.9° |
| RenaudinExtmag |
7.9° |
7.8° |
14.9° |
54.8° |
| RenaudinSn |
20.1° |
20.4° |
34.8° |
86.5° |
| Sabatini |
8.0° |
8.1° |
15.3° |
49.5° |
| SabatiniExtacc |
10.8° |
11.4° |
19.6° |
52.3° |
| SabatiniExtaccExtmag |
10.8° |
11.4° |
19.6° |
52.3° |
| SabatiniExtmag |
7.7° |
7.8° |
14.9° |
49.4° |
Table 10. Precision according to sampling with all motions and with/without magnetic perturbations.
Balance between the precision and the stability
*Stability is a moving STD with a window of 0.1s.












